Rise, Set, Ebb, Flow, Breathe, Grow

A computer generated art installation of evolving fractal geometry

Owen Kaluza, 2016

Hargrave-Andrew Library, Monash University, Clayton Campus http://monash.edu/news/show/new-library-exhibition

About the works

There are 10 individual animated sequences, which I selected to fit with the theme of imitating natural processes and forms, and to perhaps evoke a reminder of the outside world in an indoor environment.

The first group of six attempt to mirror outdoor scenes and landscapes, the flowing water of tides and ocean waves feature in the first two.

“Tidal Flow” “Pacific Coast”

The third and fourth mimic the crossing paths of the sun and moon with associated changes in light.

“Sunrise-Sunset”

“Moonrise”

The fifth work shows repeating cloud-like patterns representing changing light and passing time.

“Painted Clouds”

Next comes a rapidly transitioning landscape scene that recalls the movement of sand dunes or the processes of weather and erosion in shaping the earth.

“Dust Storm”

In the last four animations we deviate to more abstract forms, with branching, symmetric, tree-like shapes, morphing in cyclical patterns, hinting at growth over time through the variation of seasons.

“Circle Breathe”

“Corymbia”

“Sand and Sky”

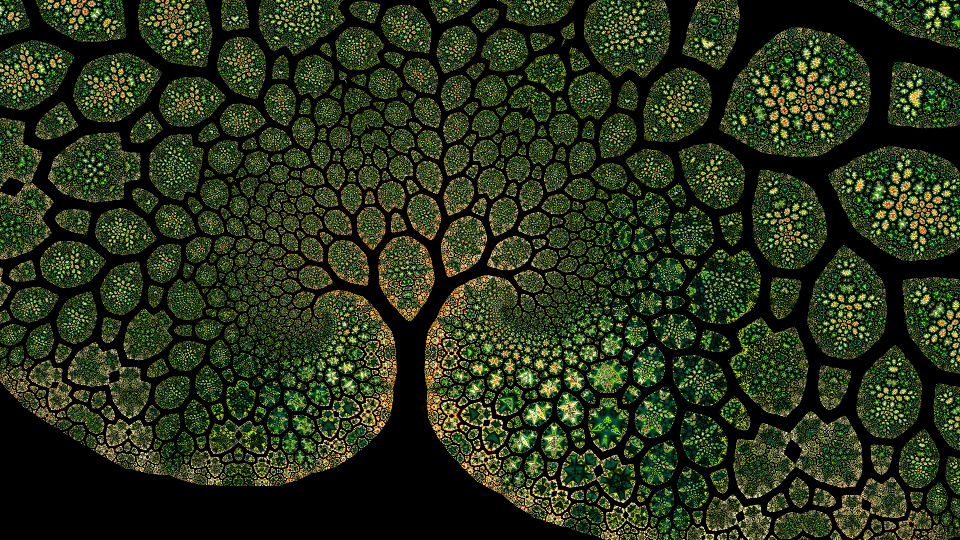“Fractured Tree”

I designed several individual pieces so that the repetition of animated sequences within have a slower cycle overlaid with a higher frequency repeating cycle.

This creates a hypnotic element to the cycling patterns which I find pleasantly meditative, combining repeating and continuously varying elements in a form of repetition with variation that is the hallmark of the fractal images they are derived from.

I attempted to increase the relaxing quality of the works by aligning the repeating frequencies with a deep breathing pace.

Lastly, I set the total length of the exhibition to exactly 48 minutes, so that it would line up with the hour, every 4 hours at 2, 6 and 10 and the same specific animation will be playing at the same time every day.

Why: Theme, motivation, concept

A core concept of this work is the evocation of the natural world using imagery that contains familiar shapes but which are at the same time, quite strange.

I’ve attempted to highlight where patterns from the natural world sprang out of the mathematical worlds under exploration. The aim is to echo familiar forms and use naturally inspired colours whilst creating images that are still something different from the natural world - any observer can see they could only have been produced artificially with the aid of a computer but the natural inspiration is hopefully also obvious.

I particularly enjoyed trying to create scenes evocative of landscapes. It’s a challenge because fractal patterns often look alien and unreal but there are still many underlying familiar patterns of nature to be found.

Much of our lives are now centred around technology and computers and less time is spent in the natural world.

Even as a technology enthusiast, I often find myself frustrated by the amount of time I must spend indoors, a common complaint I’m sure - and computer science doesn’t offer many opportunities for fieldwork.

Hopefully we’ll manage to reach some level of sustainability in the future so enjoying parts of the non-human natural environment that have not been excessively modified by humans is still possible.

As an aside, the irony of spending so much time hunched in front of a computer over the years attempting to amplify a faint echo of nature in the artificial glow of pixels on a screen is not lost on me.

Despite this I found it a very enjoyable escape, I could take a break from study or work and play with an image for a while - for me it was a type of process art, where the act of producing it was the most important aspect at the time.

I wonder if the infinite detail, chaotic patterns and self-similarity of some fractal based images can perhaps trigger something primal in the brain that has a similar effect to looking at a landscape of natural features. It seems to make one able to look at an image longer without getting bored, like your brain is waiting to see something alive moving off in the distance.

How: Technique - Mathematical, Computational

To explain a little background about the techniques used, this is a type of computer generated, algorithmic art, based on “fractals” – which I’m sure everyone has heard of and seen images of before.

Fractals are, by definition - patterns produced in nature or by mathematical formulae that do not just repeat, but repeat at every scale, if you zoom in you’ll eventually see the same patterns occurring again and again. Spirals and branching patterns are common examples.

The class of mathematical formulae I started with to produce these images are related to the Mandelbrot and Julia sets - visualisations of the behaviour of iterated complex polynomials arising from the field of Complex Dynamics.

Their forms were gradually uncovered over the last century beginning with the work of Pierre Fatou and Gaston Julia,

The first computer visualisation of this fractal world was seen by Benoit Mandelbrot in the 70s - later reaching public awareness as a scientific discovery and exhibited as art in the 80s.

They were discovered as a mathematical curiosity, not as an attempt to describe or model a natural phenomena but many similarities between them and naturally occurring patterns have been found since.

So this stuff has been around a while, and certainly the original formulae are not a new or very fashionable technique, in fact largely they’ve been left behind as generative and algorithmic artists moved on to newer techniques.

However, what we’re looking at is definitely quite original and could never have been produced last century.

Each point of the image is generated by iterating a formula in the complex number domain which appears deceptively simple but often exhibits wildly chaotic behaviour.

A huge number of parameters of the formula can be changed to send it off in strange new directions.

A chosen colour palette can then be applied with a number of further algorithms to produce the final image based on both the terminating value and path taken through the complex plane.

This process for computing the colour for each of millions of tiny pixel takes hundreds or thousands of computations and to work creatively requires changing parameters and colours so repeatedly generating new images.

This used to be a painstakingly slow process and images were generally only produced a single frame at a time.

When I first started writing software to produce these images over 10 years ago, my amateurish program would take a minute or two to produce even a single 500 x 500 square image on my old desktop pc, if I wanted to produce a large high-quality image I would have to go away and leave the machine working for a few hours.

Recent advances in graphics processor technology have allowed massive acceleration of the computations involved. This has really opened up huge areas of abstract mathematical worlds that would have taken years to explore before.

We have the computer games industry to thank for making these processors mass produced, cheap and readily available. Because of this you can now have the processing power of a supercomputer from the early 2000s for your home desktop for a few hundred dollars.

For comparison, I was able to render one of these high-definition sequences of around 10,000 frames in about an hour on a GPU powered machine. So that’s roughly 10,000 times faster or 4 orders of magnitude in 10 years.

I developed a web based fractal studio application that utilises this technology a few years ago, this has been central to being able to explore these forms in a creative and fluid way.

With the huge increases in rendering speed, the interaction of modifying parameters could be connected to a mouse scrolling action or a touchscreen on an attached device, allowing a much more fluid approach to exploration.

How: Design & Process

Of course it’s not just raw computing power, in that time I’ve spent exploring and getting to this point I’ve found a lot of unique structures and interesting patterns to use as raw material, and by their nature fractals produce infinite possibilities, which can never be fully explored or exhausted as they are infinite universes in their own right.

Working with fractals as a medium of art has been compared to photography in that you are framing and manipulating a source of imagery that is pre-existing in some form. With drawing I’ve always had trouble deciding what to start working on. With fractals you never have that blank canvas problem, you can just start in an exploratory fashion, playing with a formula and sculpting the inputs until you find a new virtual space, then moving through infinite regions until something piques your interest.

Over time I’ve twisted and tortured old formulae out of shape or come up with entirely new ones and ended up with a vast library of saved curiosities which can be retrieved and worked on more creatively. Many of them echo an aspect of nature or just simply have a pleasing symmetry or pattern. I like the idea of a museum catalogue of strange forms, like in the plates of Kunstformen der Natur of German biologist and artist Ernst Haeckel.

With imagination and repeated attempts at working with one of these raw forms, gradually an aesthetically pleasing result can be drawn out.

I definitely find a temptation to overdo the colours in computer generated imagery, my first images were more like psychedelic nightmares looking back but I think I’ve gotten better at toning the saturation and colour variation down over the years - nature is usually more subtle.

The ability to do animation enabled by increased computing speed adds another dimension to the work, allowing some of the adjustments, whether to colour or other input parameters to be changed over time, bringing them to life.

Essentially, producing these works based on iterative algorithms has been itself an iterative process of improvement over a period of years, you could say it was almost fractal in nature.

Appendix A: Links and more information

Monash Insider article

Library blog article

I have some old work up here where prints can be purchased, it urgently needs to be updated with some new work however!

Appendix B: Software used

The main tool I used was this web application I developed a few years ago: http://fract.ured.me.

It was a hobby project that had the aims of :

1) Creating studio software to improve and capture my own workflow of creating art using a web based graphical user interface and the speed of the graphics processing unit to allow much more fluid creative expression.

2) Bringing GPU powered fractals to a wider audience and provide a platform for sharing and collaborating.

However I completely failed to promote it effectively and it was only successful in the first goal.

The documentation is also a little lacking, but the main innovations apart from utilising the GPU via WebGL are that the formulae have been very heavily generalised, so a single formula opens up a multitude of derived formulae and actually allows you to interactively invent new formula by selecting different options to warp and transform its behaviour.

The major limitation is that WebGL only allows the use of single precision floating-point numbers, so you are very limited in how far you can zoom. I implemented a double precision version in WebCL but sadly this standard seems to have died so is no longer usable.

This doesn’t impact me too much as I prefer exploring fractal spaces more “breadthwise” to find new forms rather than zooming to incredible depths. After all, by their nature, fractals just start to repeat a lot if if you just keepin zooming in.

Hopefully in the future I will finish and release the server based version that will open up further zoom capability.

It also has a basic scripting capability in javascript that allows animations to be created.

Most of the images use a variation of the various smooth or exponential smoothing colouring algorithms found in commonly available fractal software as implemented in fractured.

Sometimes these formulae have also been modified to achieve differing results but the real effort in the colouring effects has been in carefully constructing a palette to highlight the desired areas of the patterns produced. The palette editor in fractured allows visual modification of the colours applied with some features to make it easier to quickly try new combinations such as scrolling or cycling the palette.

The videos for the exhibit were done with an additional piece of software that takes fractal programs generated by fractured, renders them with a provided set of parameters in high resolution and records the result as a video frame. This allowed the animations produced in scripts in fractured to be recorded in HD video format.

I do intend to release the source code to these tools but the repositories are not currently open as I need to do a bit of housekeeping first.

Appendix C: The mathematical formulae used

I’m listing here the starting points and inspirations for the formulae used but the actual formula have various transformations and adaptations made through the creative process of producing the final images.

“Tidal Flow”

Uses a heavily warped version of the classic Mandelbrot Set formula \(z_{n+1} = z_n^2+c\)

“Pacific Coast”

A modification of a formula called the Cactus Fractal

\[z_{n+1} = z_n^3 + z_n(z_0 - 1) - z_0\]

“Painted Clouds”

This has a variation of the “Nova” fractal as a starting point, which itself is a generalisation to a Mandelbrot set type fractal of the Newton fractal a form of Julia set which visualises Newton’s method applied to a fixed polynomial in ℂ \(z_{n+1} = z_n - \frac{rz_n^p-1}{dz_n^{p-1}} + c\)

“Sunrise to Sunset”, “Moonrise”, “Circle Breathe”, “Corymbia”, “Sand and Sky”

These works use a highly generalised version of a formula from a family of fractals that come from theoretical physics studies of magnetism called the Magnet fractals (also here, here and here).

Based on a formula named “Magnet 3” in software such as Xaos and Gnofract4d, also appears somewhat like a Möbius transformation formula. Also related to the Kleinian Group Fractals (see also).

It is of course further generalised and warped in my implementation in Fractured.

\[z_{n+1} = \frac{az_n^p+b}{dz_n^p+e} + c\]

“Fractured Tree”

This work is also based on a “Magnet” family fractal, published in most fractal software as “Magnet 1”.

\[z_{n+1} = \frac{z_n^2+(c-1)^2}{2z_n+(c-2)}\]

Appendix D: Colouring algorithms

A paper on the topic http://www.mi.sanu.ac.rs/vismath/javier/

In fractured, the basic colouring options are as follows:

Where: μ [0,1] is the colour palette selection n = number of iterations performed before bailout (or upper bound reached) t = upper bound of iterations b = bailout radius² parameter (default 4.0) p = power parameter (default 2.0)

Default (Escape time) \(\mu = \frac{n}{t}\)
Smooth (Normalised Iteration Count): \(\mu = \frac {r}{t}\) where: \(r= n + 1 - \frac{log(log(\|z_n\|))}{log(p)}\) or \(r = n + \frac{log(log(\sqrt{b})) - log(log(\|z_n\|))}{log(p)}\)
Exponential Smoothing, divergent: \(\mu = \frac {s}{t}\) where: \(s = \sum\limits_{z=z_0}^{z_n} e^{-\lVert z \rVert}\) and convergent: \(s = \sum\limits_{z=z_0}^{z_n} e^{\frac{-1}{\|z\|}}\)
Triangle Inequality: \(L = \Bigl\lvert \|z-c\| - \|c\|\Bigr\rvert\) \(A = \frac{\Bigg[ \sum\limits_{z=z_1}^{z_n} \frac{\|z\| - L}{\|z-c\| + \|c\| - L} \Bigg]}{n}\) \(B = \frac{\Bigg[ \sum\limits_{z=z_1}^{z_{n-1}} \frac{\|z\| - L}{\|z-c\| + \|c\| - L} \Bigg]}{n-1}\) \(\mu = B + (A - B) \Bigg[\frac{log(\frac{log(b)}{2}) - log(log(\|z_n\|))}{log(p)} + 1\Bigg]\)
Gaussian Integers: (average distance variant shown) \(\mu = \frac{ \Big[ \sum\limits_{z=z_0}^{z_n} \|z-round(z)\| \Big] }{n}\)